2진수, 8진수, 10진수, 16진수 변환 방법

2진수, 8진수, 10진수, 16진수

2진수란?

2진수 또는 2진법이라고 해서 '0'과 '1'로 이루어져 있는 수를 말합니다.

많이들 기계어라고 해서 하드웨어적인 관점에서 보면 전기가 있고 없음으로,

전기가 흐르고 있으면 '1', 흐르지 않고 없으면 '0'이라고 표현을 하게 됨으로 하드웨어에서는 무수한 2진수들로 이루어져 있다고 할 수 있습니다. 2진수의 예시로 10진수 '10'을 2진법으로 표현을 하면 '1010'이 됩니다.

 

8진수란?

8진수 또는 8진법이라고 해서 컴퓨터 분야에서 숫자를 표현하기 위해서 쓰이게 되었다고 합니다.

예전에는 8bit 컴퓨터를 시작으로 비트 단위의 프로그램이 활성화되어 있어서 사용하게 된 것이 아닌가 유추해 봅니다.

8진수는 '0, 1, 2, 3, 4, 5, 6, 7'로 이루어져 있습니다. 예시로 10진수 '10'을 8진법으로 표현을 하면 '12'가 됩니다.

 

10진수란?

10진수는 우리가 가장 일반적으로 사용을 하고 있는 숫자 표현법으로 '0, 1, 2, 3, 4, 5, 6, 7, 8, 9'로 이루어져 있습니다.

 

16진수란?

16진수 또는 16진법 또는 'HEX'라고 표현을 합니다.

8진수와 마찬가지로 컴퓨터 분야에서 많이 사용을 하고 있습니다.

오히려 8비트에서 16비트로 진화하면서,

저의 개인적인 견해로는 8진수 보다 더 많이 활용하고 사용하는 진법 중의 하나라고 생각됩니다.

실제로 현업에서 많이 사용을 하고 있습니다.

16진수는 '0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F'로 이루어져 있습니다.

9 다음 10부터는 알파벳을 사용하여, 10은 'A', 11은 'B', 12는 'C', 13은 'D', 14는 'E', 15는 'F'로 표현을 합니다.

숫자 2와 숫자 14를 표현하는 E가 발음상 겹치는 부분이 있어서 제 주변분들은 모두 '에코'라고 표현을 합니다.

 

2진수와 10진수 변환 관계

2진수와 10진수의 변환 관계를 알아보겠습니다.

2진수를 10진수로 변환하는 법은 2진수는 0, 1로 이루어져 있으므로,

자릿수 올림으로 0, 1, 10, 11, 100, 101 식으로 자릿수를 올리면서 숫자가 증가함을 알 수 있습니다.

각각의 자릿수는 2의 n승으로서 0의 자리는 2의 0승, 1의 자리는 2의 1승이 됩니다.

2진수 '0111 1011'을 10진수로 표현을 하면 2의 n승한 값에 그 자릿수를 곱하여 나온 값을 전부 더하면 10진수로 변환됩니다.

반대로 10진수를 2진수로 변환을 하는 방법은

10진수의 수를 2로 나누어서 더 이상 2로 나누어 떨어지지 않을 때까지 '나누어 나온 남은 몫과 나머지'입니다.

 

 

8진수와 10진수 변환 관계

8진수와 10진수의 변환 관계를 알아보겠습니다.

8진수를 10진수로 변환하는 법은 8진수는 0, 1, 2, 3, 4, 5, 6, 7로 이루어져 있으므로,

자릿수 올림으로 0, 1, 2, 3, 4, 5, 6, 7, 10, 11, 12, 13식으로 자릿수를 올리면서 숫자가 증가함을 알 수 있습니다.

각각의 자릿수는 8의 n승으로서 0의 자리는 8의 0승, 1의 자리는 8의 1승이 됩니다.

8진수 '173'을 10진수로 표현을 하면 8의 n승한 값에 그 자릿수를 곱하여 나온 값을 전부 더하면 10진수로 변환됩니다.

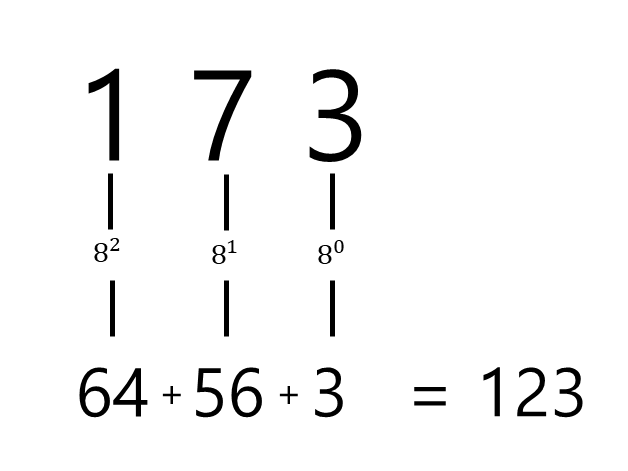
반대로 10진수를 8진수로 변환을 하는 방법은

10진수의 수를 8로 나누어서 몫이 더 이상 8로 나누어 떨어지지 않을 때까지 '나누어 나온 남은 몫과 나머지'입니다.

 

16진수와 10진수 변환 관계

16진수와 10진수의 변환 관계를 알아보겠습니다.

16진수를 10진수로 변환하는 법은 16진수는 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F로 이루어져 있으므로,

자릿수 올림으로 0, 1, 2, 3, 4, 5, 6, 7, A, B, C, D, E, F, 10, 11식으로 자릿수를 올리면서 숫자가 증가함을 알 수 있습니다.

각각의 자릿수는 16의 n승으로서 0의 자리는 16의 0승, 1의 자리는 16의 1승이 됩니다.

16진수 '7B'를 10진수로 표현을 하면 16의 n승한 값에 그 자릿수를 곱하여 나온 값을 전부 더하면 10진수로 변환됩니다.

 

반대로 10진수를 8진수로 변환을 하는 방법은

10진수의 수를 8로 나누어서 몫이 더 이상 8로 나누어 떨어지지 않을 때까지 '나누어 나온 남은 몫과 나머지'입니다.

 

 

윈도우 계산기 사용 팁

저는 암산이 약해서 인지, 가끔 헷갈리기도 합니다. 프로그램을 오래 하신 분들은 바로 척척 나오는 모습을 신기하게 봅니다.

오늘 현장에서 설명하다가 갑자기 당황을 해서인지 어리바리해서 오늘 정리를 할 겸 해서 이렇게 포스팅을 하게 되었습니다.

아무래도 계산기의 노예가 되어서 머리를 안 쓰다 보니 그런 거 같습니다.

자주 쓰는 수는 공식처럼 머릿속에 외우고 있는데, 그렇지 않은 수가 나오면 계산기를 찾아서 사용을 합니다.

스마트폰 앱으로도 변환해주는 계산기가 있는 것으로 알고 있습니다.

윈도우 계산기 사용법

하하~ 그래도 가끔은 머리를 써주는 것이 건강에 좋다고 하네요. 너무 계산기에 의존하지 마세요^^

 

저의 글을 읽어 주셔서 감사합니다. 오늘도 즐거운 하루 보내세요.

저의 글이 조금이나마 도움이 되셨다면 로그인이 필요 없는 공감♥ 한번 꾸욱 눌러주세요 하하~